décembre 2016 – Divagations

Père Noël : le grand secret

25 décembre 2016 Physique Comments 0 Comment

Au moment où cet article est publié, le Père Noël est en pleine distribution de cadeaux, parcourant le monde à bord de son traîneau. Et là, en tant que scientifique rationnel, cela soulève tout un tas d’interrogations : comment tout cela est-il possible ? Petite étude à partir de divers éléments à notre disposition, qui nous permettra peut-être de percer certains mystères de cet être méconnu qu’est le Père Noël.

Trajet

Le Père Noël parcourt le monde pour offrir des cadeaux aux enfants, durant la nuit du 24 au 25 décembre. Cela signifie donc qu’il dispose d’une heure pour parcourir chaque fuseau horaire (à peu près, les humains étant suffisamment casse-couilles pour créer des fuseaux en décalage d’une demi-heure ou d’un quart d’heure). On peut donc tracer un trajet approximatif du Père Noël durant son périple.

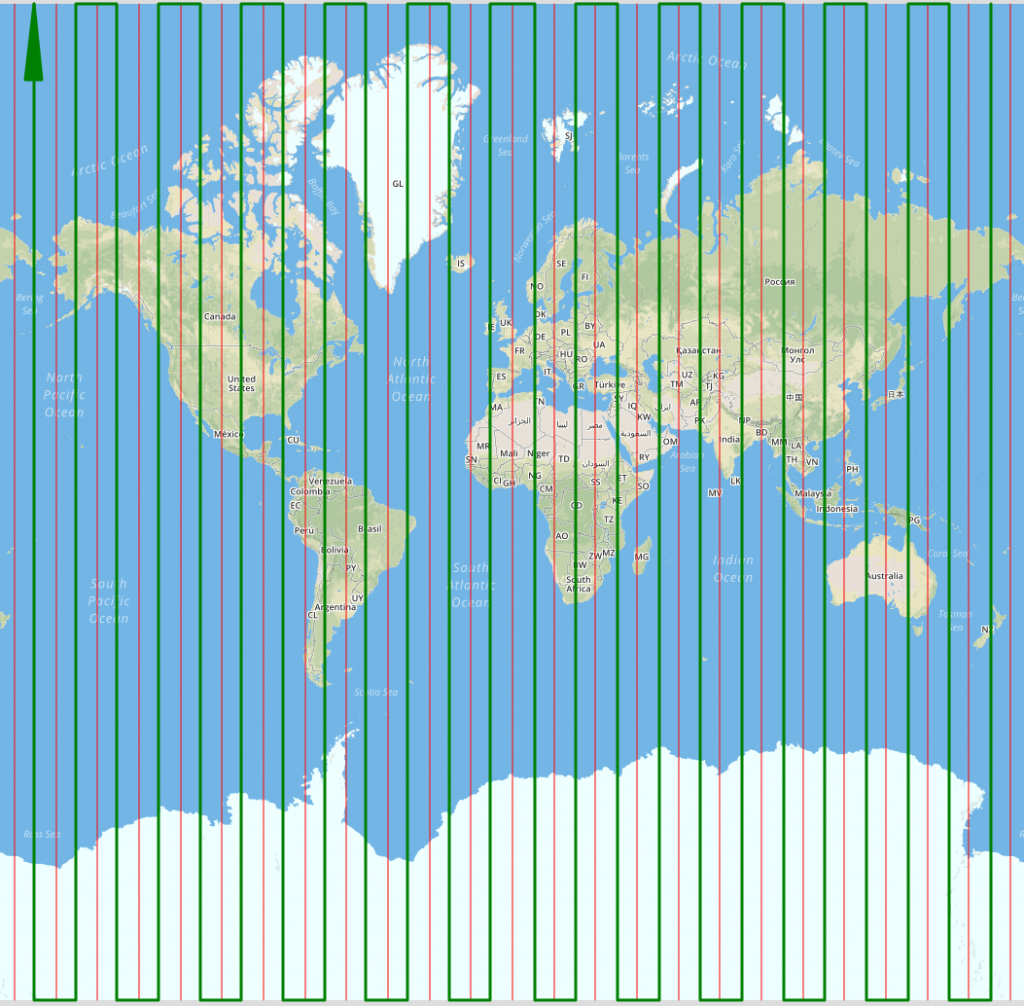
Sont délimités en rouge sur ce planisphère les 24 fuseaux considérés et est représenté en vert le trajet du traîneau. On se retrouve donc avec 24 «segments» (en considérant la Terre comme étant une sphère, ce ne sont bien sûr pas des segments mais des arcs de cercle) reliant les pôles Nord et Sud. On supposera que le Père Noël dispose à chaque pôle d’une station lui permettant de faire le plein, de recharger des cadeaux… voire, plus pratique, de changer de traîneau dès son arrivée pour pouvoir repartir sur le champ, ~~ses sbires~~ ses lutins ayant alors deux heures pour remettre le traîneau restant sur place en état de marche. Chaque segment correspont à la moitié d’une circonférence terrestre, ce qui représente une distance à parcourir de 20000 km; on se retrouve donc avec une distance totale de 480000 km.

Vitesse et accélération

Du trajet défini ci-dessus, on en déduit rapidement la vitesse moyenne du traîneau. Les 20000 km d’un méridien sont parcourus en une heure, ce qui nous donne trivialement une vitesse moyenne de 20000 km/h.

Cependant, ceci n’est qu’une vitesse moyenne. En effet, en partant d’un pôle, le traîneau part d’une vitesse nulle : il lui faut alors accélérer jusqu’à atteindre une vitesse de croisière, puis freiner juste avant son arrivée pour pouvoir s’arrêter à l’autre pôle. Et tout Père Noël qu’il soit, il ne peut pas supporter une accélération au dessus d’un certain seuil et il lui faudra donc un certain temps non négligeable pour atteindre sa vitesse de croisière.

On peut ainsi définir trois parties dans le voyage du traîneau le long d’un fuseau :

accélération durant un certain temps que l’on notera `t_a`;
vol à vitesse constante (et donc à accélération nulle) une fois la vitesse de croisière atteinte;
décélération avant d’arriver au pôle, on considérera cette décélération exactement opposée à l’accélération initiale et donc également de durée `t_a`.

La valeur de l’accélération sera notée `a` et on prendra comme valeur numérique `a=39 m.s^(-2)`, correspondant à une accélération de 4g : cette valeur correspond à l’accélération normalement subie par des astronautes à bord d’un Soyouz lors de son décollage. On peut alors déterminer `a(t)`, représentant l’accélération du traîneau en fonction du temps :

`a(t)=a` pour `0<=t<=t_a`;
`a(t)=0` pour `t_a<=t<=t_d`;
`a(t)=-a` pour `t_d<=t<=T`.

Instant notation : dans ces équations et celles à suivre, `t_d` est l’instant où commence la décélération et `T` la durée totale du trajet. On a défini `T=3600s` et, la décélération étant de même durée que l’accélération, on en déduit donc `t_d=T-t_a`.
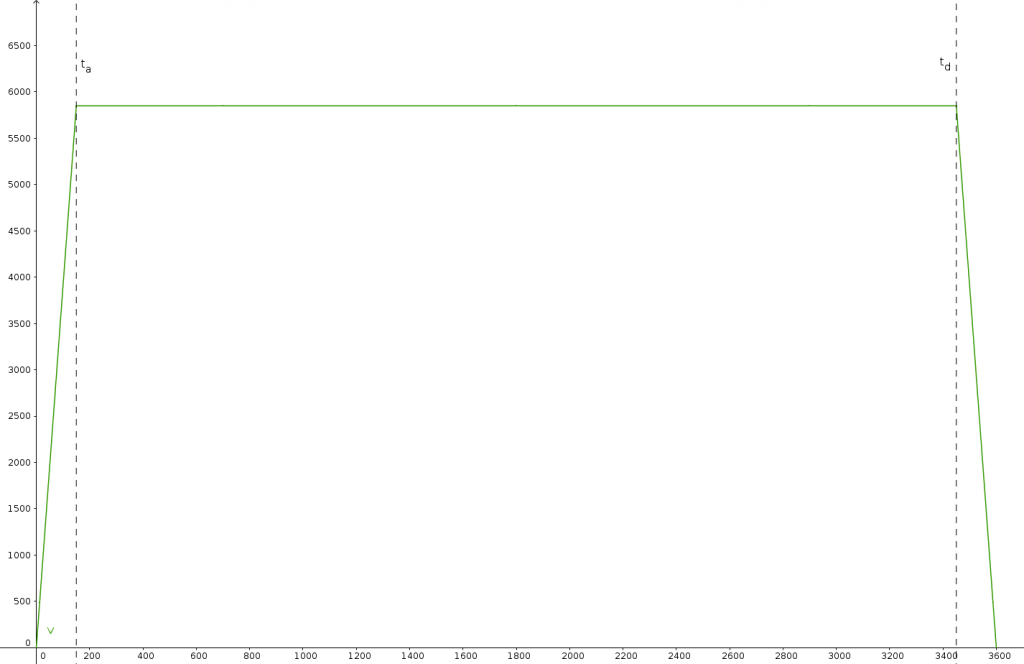
Pour passer de l’accélération à la vitesse, il suffit d’un coup de primitive, ou plutôt de trois vu que l’accélération est définie en trois parties. On peut ainsi définir la fonction `v(t)` représentant la vitesse au cours du temps, toujours en trois parties.

`v(t)=at` pour `0<=t<=t_a`.
`v(t)=V` pour `t_a<=t<=t_d`.
`v(t)=aT-at` pour `t_d<=t<=T`.

On n’oublie pas non plus que l’utilisation de la primitive ajoute des constantes : ici, le calcul est trivial est n’est donc pas détaillé mais ça ne sera pas le cas au tour suivant (oh, teasing) (et au pire, vous pouvez vérifier le calcul par vous même, interactivité, web 2.0, toussa toussa). C’est ainsi qu’apparaît `V` la vitesse maximale atteinte en `t_a`, ce qui nous donne `V=at_a`.

Voici une représentation graphique de cette fonction `v(t)`, définie entre `0` et `T`.

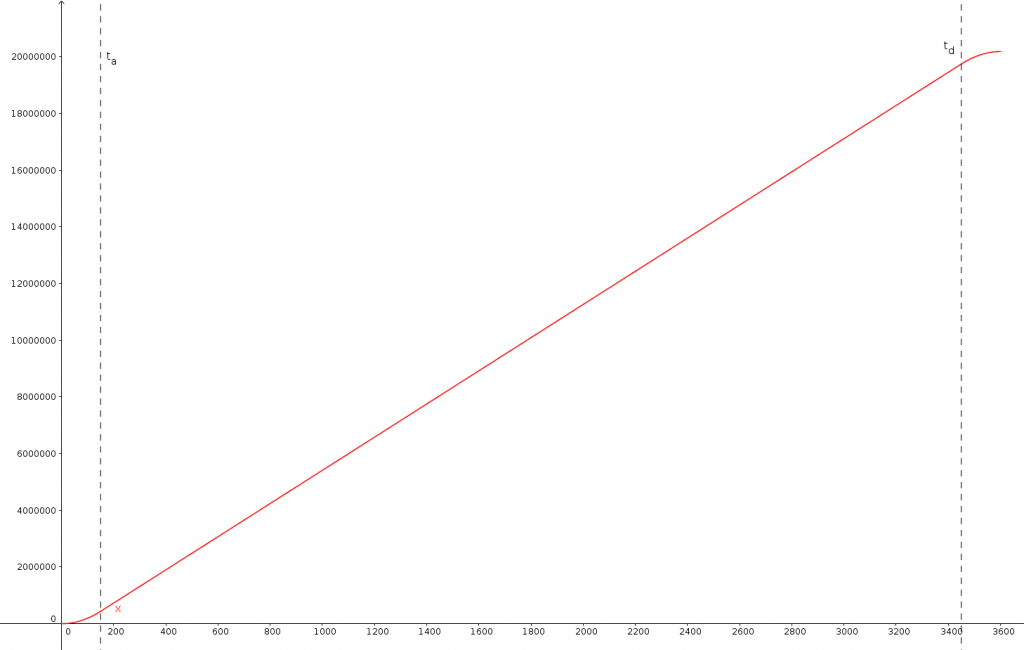
On peut passer maintenant à la fonction `x(t)`, définissant la position du traîneau le long du méridien selon le temps. Là encore, triple primitivisation (mon correcteur orthographique me dit que ce mot n’existe pas, mais ça devrait). Ce qui nous donne :

`x(t)=(at²)/2` pour `0<=t<=t_a`;
`x(t)=Vt+C_1` pour `t_a<=t<=t_d`;
`x(t)=-(at²)/2+aTt+C_2` pour `t_d<=t<=T`.

La fonction `x(t)` est représentée ci-dessus. On note bien cette fois les constantes `C_1` et `C_2` apparues lors du calcul de la primitive. Il nous faut donc maintenant les calculer, en utilisant le fait que notre fonction est continue (le traîneau ne se téléporte pas lorsqu’il arrête son accélération ou entame sa décélération (dommage, ça serait rigolo)).

Ainsi, en calculant `x(t_a)`, on obtient `(at_a²)/2=Vt_a+C_1`. Après avoir rappelé que `V=at_a`, on peut dérouler le calcul.

`(at_a²)/2=at_a²+C_1`

`C_1=-(at_a²)/2`

On passe à la seconde constante, en calculant `x(t_d)`.

`Vt_d-(at_a²)/2=-(at_d²)/2+aTt_d+C_2`

`C_2=at_at_d-aTt_d-(at_a²)/2+(at_d²)/2`

`C_2=at_d(t_a-T)-(at_a²)/2+(at_d²)/2`

`C_2=-at_d²-(at_a²)/2+(at_d²)/2`

`C_2=-(at_a²)/2-(at_d²)/2`

`C_2=-(a(t_a²+t_d²))/2`

Vient enfin le moment de calculer `t_a`, qui nous permettra de déterminer tout le reste. On va utiliser pour cela la distance parcourue au total qui est de 20000 km et qui correspond donc à `x(T)`. Histoire de ne pas trop encombrer nos calculs, on notera `X=20000 km` cette distance totale, ce qui nous donne `x(T)=-(aT²)/2+aT²-(a(t_a²+t_d²))/2=X`.

`X=(aT²)/2-(a(t_a²+t_d²))/2`

`X=(a(T²-(t_a²+(T-t_a)²)))/2`

`X=(a(T²-(t_a²+T²-2Tt_a+t_a²)))/2`

`X=(a(-2t_a²+2Tt_a))/2`

`at_a²-aTt_a+X=0`

Une équation du second degré apparaît ! Cyril utilise Discriminant.

`Delta=a²T²-4aX`

On a comme valeurs numériques `a=39m*s^(-2)`, `T=3600s` et `X=2*10^7m`, ce qui nous donne `Delta=16592160000>0`. C’est très efficace ! L’équation est KO. Cyril gagne deux résultats réels : `t_a=(aT+-sqrt(Delta))/(2a)`.

D’un côté, on a `(aT+sqrt(Delta))/(2a)=3451.4s`, ce qui est problématique puisqu’on préférerait obtenir une valeur nous laissant le temps d’accélérer puis de décélérer sur la durée du trajet.

Deuxième essai : `(aT-sqrt(Delta))/(2a)=148.6s`. Beaucoup mieux, on prend !

Bonus : on peut remarquer que la somme de nos deux solutions vaut 3600 et donc que la première valeur obtenue correspond à `t_d` ! On peut aisément vérifier que remplacer `t_a` par `t_d=T-t_a` dans l’équation ne change rien à cette dernière.

On obtient donc une phase d’accélération d’environ deux minutes et demie, permettant d’atteindre la vitesse `V=at_a=5794.7m.s^(-1)=20861 km.h^(-1)` maintenue pendant 55 minutes, puis une décélération avant l’arrivée. La vitesse maximale est donc à peu près de Mach 17, produisant un léger bang supersonique.

Cadeaux

Une fois le trajet défini, passons au contenu du traîneau : les cadeaux ! Oui, mais combien de cadeaux ? Si le Père Noël est vraiment un type cool, il doit apporter un cadeau à tous les enfants de l’humanité. On considérera les morveux de 0 à 14 ans; il n’y a plus qu’à les compter. Ça tombe bien, l’ONU l’a déjà fait (United Nations, Department of Economic and Social Affairs, Population Division (2015). World Population Prospects: The 2015 Revision, custom data acquired via website, je vous laisse farfouiller pour retrouver les données). On trouve un total de 1.930.760.000 petits nenfants et donc autant de cadeaux.

Intéressons-nous aux cadeaux en eux-même maintenant. On va considérer chaque cadeau comme ayant une masse de 100g et une masse volumique équivalente à celle de l’eau (`1000 kg*m^(-3)`).

Du côté de la masse, ça nous donne un total de `1930760000xx100=193076000000g=193076t`. On peut ensuite diviser par 24 pour obtenir la quantité de cadeaux distribuée dans un fuseau horaire, ce qui nous donne 8045 tonnes par chargement.

Et niveau place, dans tout ça ? Trivial : en considérant qu’une tonne de cadeaux occupe un mètre cube au vu de la masse volumique considérée, ça nous donne 193076 m³ pour tous les cadeaux et 8045 m³ sur un fuseau.

On pourra comparer ces résultats avec un A380 par exemple, proposant environ 1200 m³ pour ses passagers et leurs bagages, pour une charge pouvant aller jusqu’à 100 tonnes.

Énergie

Le traîneau est prêt et chargé, le trajet a été défini, on peut partir maintenant ? Presque, il faut juste un peu d’énergie pour faire le trajet.

Encore une fois, la consommation du traîneau va se découper en trois phases (oui, toujours les mêmes, en même temps y a pas de raison que ça change) : accélération, maintien de la vitesse et décélération.

Commençons par étudier la phase intermédiaire du trajet, à vitesse constante. Si le traîneau voyageait dans l’espace intersidéral, il n’y aurait rien à faire mais sur Terre, il doit faire face au frottement de l’air, entraînant une force de traînée opposée à son mouvement; le traîneau va donc devoir compenser cette force. (Il y a aussi le poids du traîneau à considérer, engendrant une force verticale vers le bas; on dira que le traîneau est super badass et qu’il est taillé de telle façon que sa portance compense parfaitement son poids.)

L’intensité de cette force de traînée est `T=1/2rhoSC_xV²`, avec :

`rho` la masse volumique de l’air, valant `rho=1.293 kg.m^(-3)`;
`S` la section transversale du traîneau faisant face au mouvement, on a calculé juste avant un volume nécessaire de 8045 m³, on estimera donc les dimensions du traîneau à `10mxx10mxx80.45m`, ce qui nous donne une section `S=100m²`;
`C_x` le coefficient de traînée du traîneau, on supposera que le Père Noël est super doué et a fait en sorte que son traîneau dispose d’un coefficient de traînée faible en prenant `C_x=0.01`;
`V` la vitesse, qu’on a calculé auparavant, `V=5794.7m.s^(-1)`.

On vérifie que les unités sont uniformes, on calcule tout ça et on obtient `T=21708531N`. Ne reste plus qu’à calculer l’énergie nécessaire pour créer une force de même intensité et pour cela, il suffit de multiplier `T` par la distance sur laquelle est appliquée cette force. Alors alors, cette distance `d` est parcourue à la vitesse `V` sur une durée `T-2t_a`; mon petit doigt me dit qu’on a `d=V(T-2t_a)=19138735m`. Notre énergie consommée lors de la phase à vitesse constante est donc `E_c=Td=4.1547*10^(14)J=115410 MWh`.

L’énergie nécessaire pour l’accélération, maintenant. On ne va pas tenir compte de la traînée dans cette partie, d’une part parce que ce post est déjà bien trop long mais surtout parce que, avec une vitesse qui n’est plus constante, ça devient chiant à calculer (comment ça, la flemme ? :p). Donc, pour donner une accélération `a` à notre traîneau, il faut lui appliquer une force d’intensité `F_a=ma`. On a toujours `a=39m.s^(-2)`. Pour la masse, il s’agit de la masse du traîneau, c’est à dire de la masse des cadeaux et de celle du traîneau à vide. On va de nouveau faire l’analogie avec un A380 et considérer une masse à vide équivalente; on estimera ainsi la masse du traîneau à vide à 300 tonnes. Ce qui nous donne `m=8.345*10^6 kg`. On obtient donc au final `F_a=325455000N`. Cette force s’applique lors de l’accélération, soit sur une distance `d’=(20000000-d)/2=430632.5m`. L’énergie consommée lors de l’accélération est donc `E_a=F_ad’=1.402*10^(14)J=38944 MWh`.

La décélération, ça ressemble beaucoup à l’accélération. Même distance d’application, même intensité (une décélération, c’est juste une accélération dans le sens opposé au mouvement, ça ne change rien à notre calcul); la seule différence, c’est que notre traîneau est désormais vide. On a donc `m=3*10^5kg`, `F_d=ma=11700000N` et on obtient au final `E_d=F_dd’=5.038*10^(12)J=1399 MWh`

Notre consommation totale d’énergie lors du trajet le long d’un fuseau est donc `E=E_a+E_c+E_d=155753 MWh=5.607*10^(14)J`. Après que Wikipédia nous a indiqué qu’il s’agissait de près du double de la production électrique annuelle du Togo, essayons de voir comment produire ça en une heure.

Déjà, on peut essayer de brûler des trucs. On a déjà comparé notre traîneau avec un avion, alors essayons le kérosène. Celui-ci a un pouvoir calorifique de 43,15 MJ par kilogramme; un coup de règle de trois nous permet de voir qu’il faudrait embarquer 12994 tonnes de kérosène, soit plus que le poids des cadeaux… Trouvons autre chose : ce qui donne pas mal d’énergie en brûlant, c’est l’hydrogène avec un pouvoir calorifique de 121 MJ/kg. Ça fait quand même 4634 tonnes d’hydrogène à embarquer.

Du coup, à quoi bon se trimballer des quantités gigantesques de trucs à brûler ? Et si on produisait de l’énergie à partir de panneaux solaires ? Bah malheureusement non : déjà, vu que le Père Noël passe aux alentours de minuit dans chaque fuseau, la quasi intégralité trajet se fait de nuit et donc sans Soleil (on peut juste espérer un peu de lumière du côté du Pôle Sud). Et aussi, vu que le rendement d’un panneau solaire est au mieux de 160 kWh par m² et par an, il nous faudrait 8527 km² de panneaux, soit quasiment la superficie de Porto Rico ou à peu près 80 fois la superficie de Paris… Si jamais nous venait l’idée de stocker toute cette énergie dans des batteries, nouvelle désillusion : les meilleures batteries actuelles, encore au stade de la recherche et développement, permettent d’obtenir 2,5 kWh par kilogramme; il y aurait donc besoin de 62300 tonnes de batteries…

On a essayé de brûler de l’hydrogène mais il y a quelque chose de mieux à faire : le fusionner. Plus précisément fusionner ses isotopes que sont le deutérium (un neutron en plus) et le tritium (deux neutrons en plus) : la fusion d’un atome de deutérium et d’un atome de tritium donne un atome d’hélium, un neutron et 17,6 MeV. L’électron-volt (eV) est l’unité pratique permettant de mesurer l’énergie au niveau atomique; on a `1eV=1.602*10^(-19)J`, il nous faut donc produire `3.5*10^33 eV` pour faire avancer notre traîneau.

Quoi, vous pensiez que les ordres de grandeur employés jusqu’à présent n’étaient pas assez abusés 😀 ? Allez, on va réduire tout ça en considérant l’énergie produite par une mole de deutérium et une mole de tritium. Une mole, ça contient `6.022*10^23` éléments, la fusion de nos moles de deutérium et de tritium permet donc de produire `6.022*10^23xx17.6*10^6=1.06*10^31eV`. Il ne nous suffit donc que de 330 moles de deutérium et autant de tritium pour pouvoir nous fournir l’énergie nécessaire, ce qui représente une masse totale de… 1650 grammes ! Et en plus, la réaction produit 330 moles d’hélium, soit 7,4 m³ avec des conditions normales de température et de pression, de quoi gonfler plein de ballons ! OK, on pourra opposer à cette solution que la seule application de la fusion nucléaire maîtrisée et appliquée par l’Homme est la bombe H, que la production d’énergie par fusion nucléaire en est encore au stade expérimental et qu’on est très très loin de pouvoir mettre un réacteur du genre dans un traîneau…

Conclusion

Résumons.

Le Père Noël va effectuer 24 trajets, alternativement Pôle Nord→Pôle Sud et Pôle Sud→Pôle Nord. Chacun de ces trajets dure une heure et couvre un fuseau horaire, sur une distance de 20000 km. Afin d’éviter un temps de maintenance technique à chaque arrivée à un pôle, on supposera l’existence de plusieurs traîneaux, le Père Noël se contentant de changer de traîneau à chaque étape.
Sur chacun de ces trajets, son traîneau est chargé avec 80448000 cadeaux, à distribuer à autant d’enfants. Ces cadeaux occupent un volume de 8045 m³, pour une masse de 8045 t. On laissera à la sagacité du lecteur le problème suivant : comment distribuer plus de 22000 cadeaux par seconde, tout en volant à 20000 km/h ?
Pour parcourir un fuseau en une heure, le traîneau doit subir une accélération de 4g durant une durée de deux minutes et 28 secondes afin d’atteindre sa vitesse de croisière de 20861 km/h. Il maintient cette vitesse durant 55 minutes et 4 secondes avant d’entamer sa décélération, là aussi à 4g et sur une durée de 2 minutes 28 secondes.
L’énergie nécessaire pour le parcours d’un fuseau à cette vitesse est de 560,7 TJ ou 155,753 GWh. La solution envisagée la moins encombrante pour produire cette énergie est de doter le traîneau d’un réacteur à fusion nucléaire réalisant la fusion de 660 grammes de deutérium et de 990 grammes de tritium.

On en déduit donc que le Père Noël est un gros geek, branché à fond sur les dernières technologies. Il aime voler à fond les ballons et produire des quantités d’énergie phénoménales pour profiter de ses joujoux. Il doit donc avoir un énorme compte en banque pour pouvoir se payer tout ce matos et il en profite au passage pour offrir des cadeaux et du rêve aux enfants du monde entier.

En voyant tout cela…

Mais oui, c’est limpide maintenant !

Le Père Noël…

C’est Elon Musk !

100 plaques

18 décembre 2016 Mathématiques Comments 0 Comment

Ah, les longs trajets chiants en voiture de notre enfance… Les gamins du XXI^ème siècle ne connaîtront pas ça en étant bardés de smartphones, tablettes et compagnie. À mon époque (ouais, je suis assez vieux pour pouvoir dire «à mon époque» et je vous dis flûte (politesse, quand même)), ce qui se rapprochait le plus, c’était une Game Boy mais c’était pas rétroéclairé et donc pas toujours utilisable. De même avec un bouquin : j’avais toujours un Picsou Magazine, un Science et Vie Junior ou autre à portée de main, mais je ne pouvais que constater la difficulté de lire dans un environnement mouvant et manquant de luminosité. Il y a d’autres trucs connus à faire pour s’occuper durant un trajet :

imaginer un personnage courant le long de la glissière de sécurité (perso, j’ai jamais tenu plus d’une minute);
suivre la Lune du regard (cool mais pas toujours possible selon le paysage);
identifier le département de la voiture de devant.

Pour rappel et pour les plus jeunes : avant 2009, les plaques d’immatriculation étaient au format CCCC LL CC : un nombre jusqu’à quatre chiffres, deux ou trois lettres puis le numéro du département où avait été immatriculé le véhicule, d’où le jeu. Sauf que, contrairement à mes aïeux, j’avais jamais appris la liste des départements à l’école et de toute façon, quand je vois des chiffres, je veux compter avec :).

Du coup, je me suis fabriqué mon propre jeu : utiliser les nombres présents sur une plaque pour arriver à 100. Oui, comme dans Le compte est bon :D. Évidemment, avec juste deux nombres, c’est quasiment impossible, du coup je me permettais de découper mes nombres pour en obtenir des plus petits. Ainsi, à partir d’un 1234, on peut obtenir un 12, un 123, un 23, un 34… Bien évidemment, un chiffre qui a déjà utilisé pour fabriquer un nombre ne peut pas être réutilisé et il laisse un vide : les éventuels nombres l’entourant ne fusionnent pas; si on prend le 23 dans 1234, il ne nous reste que 1 et 4, sans pouvoir former 14 (de même, les deux nombres de la plaque ne peuvent pas être collés). Et voilà de quoi s’occuper des heures \o/.

Malheureusement, les temps changent et les nouvelles plaques, au format LL-CCC-LL, se prêtent beaucoup moins à ce jeu. Et accessoirement, maintenant, c’est moi qui conduit, j’ai autre chose sur quoi me concentrer ^^. Du coup, pour pouvoir jouer facilement, j’ai fait une petite appli web, pardi !

Fonctionnement : une plaque d’immatriculation est tirée au hasard. Sur celle-ci, il est possible de cliquer sur un chiffre pour le sélectionner ou de cliquer-glisser sur une suite de chiffres pour déterminer le nombre correspondant. Une fois nos nombres choisis vient le moment de les additionner, multiplier… On choisit un nombre, l’opérateur à appliquer et un second nombre : si l’opération est valide (il faut obtenir un entier en sortie), les deux nombres choisis ne sont plus disponibles et cèdent leur place au résultat de l’opération. Et si le résultat est 100, c’est gagné ! Astuce : ma Vienne natale a une particularité, c’est le seul département dont le numéro additionné avec ses chiffres donne 100 (86+8+6); du coup, c’était un peu plus facile pour moi à l’époque ^^.

Cinq à sept

14 décembre 2016 Mathématiques Comments 0 Comment

De temps en temps arrivent sur le chan IRC du Nolife Wiki des sujets importants, comme dans ces propos d’une personne dont je tairai les multiples identités : lors d’un développement, cette boîte code un tirage aléatoire d’un entier entre 0 et 11 et, après avoir réalisé sept tirages, s’étonne d’avoir obtenu cinq fois la même valeur, s’exclame «Le hasard, c’est nul» puis sort par dépit un (1/12)⁵.

Là, mon sang de matheux ne fait qu’un tour : qu’ouïs-je ? Pourquoi cette valeur arbitraire ? Pourquoi les chapitres sur les probabilités sont-ils les derniers du programme de mathématiques de chaque année et donc non traités parce qu’il n’y a pas assez de temps ? Déterminé à en savoir plus, je décide donc de me lancer dans le calcul de cette probabilité : en tirant à sept reprises une valeur parmi douze, quelle est la probabilité d’obtenir cinq valeurs identiques ? Et tant qu’on y est, quelle est la probabilité d’obtenir X valeurs identiques ou d’obtenir sept valeurs distinctes ?

Déjà, quelques précisions et rappels.

On considère les 12 valeurs disponibles comme équiprobables : elles ont toutes la même probabilité de sortir à chaque tirage et cette probabilité est (attention, suspense ) 1/12.
Les tirages successifs se font avec remise : la valeur choisie lors d’un tirage est de nouveau disponible lors du tirage suivant. Si ce n’était pas le cas, la réponse à notre question serait triviale : 0 !
L’intitulé ne dit pas que les cinq valeurs identiques doivent être une valeur donnée ! Ce biais de réflexion est bien illustré par le paradoxe des anniversaires.
Les cinq valeurs identiques n’ont pas à être tirées à la suite : notre septuple tirage n’est pas ordonné.

Maintenant que tout ça est bien en tête, c’est parti mon kiki (ça doit bien faire deux lustres que j’ai pas utilisé cette expression :D) ! Pour répondre à notre question, nous allons créer un arbre de probabilité. Cet arbre contiendra sept niveaux, chaque niveau correspondant à un tirage. Chaque nœud ne représentera pas le tirage obtenu (l’arbre serait beaucoup BEAUCOUP BEAUCOUP trop grand et ce n’est pas ce qui nous intéresse) mais le nombre d’apparitions des valeurs tirées jusqu’alors. Petit exemple : si un nœud comporte la valeur «3-1-1», cela signifie qu’une valeur a été tirée trois fois et que deux autres valeurs ont été tirées une fois chacune; on se fiche de savoir les valeurs en question car on ne cherche pas le nombre de tirages d’une valeur donnée et parce que toutes les valeurs sont équiprobables.

Allez, c’est parti ! On prépare les sept niveaux et on commence tout à gauche.

Premier tirage, on obtient une valeur et… on obtient une valeur : il n’y a qu’un seul nœud dans l’arbre à ce niveau 1, le nœud «1». Vu qu’il n’y a qu’une seule possibilité à ce stade, on considère qu’on s’en fout pour le décomptage des probabilités, ça nous épargne un facteur 12 dans les calculs.

Niveau 2 et cette fois-ci deux possibilités. Soit on tire la même valeur que précédemment (probabilité de 1/12) et on atteint le nœud «2», soit on tire une autre valeur (probabilité 11/12) pour arriver en «1-1».
Petit point notation : les nombres sur les branches indiquent la probabilité de passage par cette branche en partant du nœud de gauche et le nombre encadré sur chaque nœud indique la probabilité d’atteindre ce nœud depuis notre nœud de départ, qui est donc le nœud «1»; la probabilité d’un nœud s’obtient en faisant la somme des probabilités venant de chacune des branches qui y mène, ces probabilités étant égales au produit du nœud de départ et de la branche empruntée. Vu que toutes les probabilités sont des multiples de 1/12 et que les dits multiples sont identiques sur toutes les branches ou sur un même niveau de nœuds, on va omettre les dénominateurs sur le schéma, histoire de l’alléger. Mais il ne faudra pas oublier à la fin de diviser le résultat obtenu par 12⁶ pour obtenir la bonne probabilité, évidemment :).

Step 3. En partant de «2», soit on tire encore la même valeur déjà obtenue deux fois pour arriver en «3», soit on en tire une autre et on tombe en «2-1». Si on part de «1-1», soit on tire une des deux valeurs déjà obtenues (probabilité de 2/12) et on va en «2-1», soit on tire une des dix autres valeurs pour se rendre en «1-1-1».

Quatrième tirage. Rien de bien nouveau en partant des nœuds «3» et «1-1-1», qui se comportent comme leurs homologues du niveau inférieur. On va plutôt détailler les branches partant du nœud «2-1». On peut soit tirer la valeur déjà tirée deux fois (1/12), soit celle tirée une seule fois (1/12) soit une des dix autres, pas encore obtenues (10/12); ce qui nous donne trois branches partant de «2-1».

On enchaîne avec le cinquième tirage et un focus sur le nœud «2-1-1». Un des 12 tirages possibles permet de passer à «3-1-1», deux envoient sur «2-2-1» (les deux valeurs déjà tirées une seule fois) et neuf mènent à «2-1-1-1» (les valeurs pas encore tirées). Maintenant que le principe est compris, le principal challenge est de ne pas s’embrouiller avec les branches qui commencent à se croiser.

On continue sur les deux derniers niveaux. Il n’y a rien de nouveau en matière de raisonnement, j’en profite donc pour donner l’arbre final.On n’oublie pas de diviser par 12⁶ pour obtenir les probabilités correspondantes. Ainsi, il y a une chance sur 12⁶ d’obtenir sept valeurs identiques (et oui, 12⁶ et pas 12⁷ car il n’y a pas de contrainte de valeur au premier tirage). Pour obtenir la probabilité d’obtenir X fois la même valeur, il suffit d’ajouter les probabilités de chaque nœud où X est la plus grande valeur présente.

Ainsi, pour obtenir cinq valeurs identiques, il y a deux nœuds correspondants : «5-2» et «5-1-1». Ce qui nous donne une probabilité de (231+2310)/12⁶, soit 0,085%.

Et voici les différentes combinaisons possibles et les probabilités correspondantes.

Sept valeurs identiques : 0,00003%
Six valeurs identiques : 0,0026%
Cinq valeurs identiques : 0,085%
Quatre valeurs identiques : 1,56%
Trois valeurs identiques : 16,89%
Deux valeurs identiques : 70,31%
Sept valeurs différentes : 11,14%

Une petite expérience pour terminer : il est possible de déterminer ces valeurs par l’expérimentation en réalisant un grand nombre de fois les 12 tirages et en notant le résultat obtenu à chaque fois. Vous pouvez faire ça à la main si ça vous amuse mais sinon, j’ai bricolé une page qui réalise les tirages toute seule. Il suffit d’indiquer le nombre de fois où les 12 tirages seront répétés (par défaut 10000 fois), de cliquer sur le bouton, d’attendre un peu si votre nombre est un peu gros et le nombre d’occurrences de chaque résultat est donné avec sa fréquence d’apparition, à comparer avec les probabilités données juste au dessus :).

Les dessous du bureau

9 décembre 2016 Loot Comments 0 Comment

Rangement, deuxième partie. Dans cet épisode : mon bureau, situé dans ma chambre et dont je ne me suis jamais servi comme bureau depuis que j’ai emménagé. Parce que je suis pas assez sérieux, je préfère taffer dans mon canapé et avec la télé en fond qu’au calme et correctement assis ^^. Mais au moins, maintenant, ça fait bureau et pas dépotoir :D.

Allez, petit tour. J’évacue les trucs chiants (la paperasse, le clavier qui traîne) ou déjà vus ici (par ici pour la numismatique) et c’est parti !

Pour commencer, mon compagnon de fac. Évidemment, en fac d’info, pas mal de monde se trimballe avec un ordinateur portable pour ~~jouer en cours~~ coder des trucs. Mais vu que le mien était pourri, je me contentais quand il n’y avait pas besoin de plus de cette tablette munie d’un dock clavier, bien plus pratique à trimballer, pour prendre des notes lors des cours où il n’y avait pas de polycopié (ce qui n’arrivait jamais).

Tant qu’on parle de cursus scolaire, voici toute la paperasse officielle, du CM2 jusqu’à mon diplôme de master. Je dois aussi avoir mes cours (oui, j’aime pas jeter) : pour le lycée voire plus vieux, c’est encore chez mes parents mais à partir de la prépa, j’ai tout à portée de main, à voir si je continue le rangement :).

À l’étage au dessus, mon principal fait d’armes : mes diplômes du concours Kangourou auquel j’ai participé durant mes années lycée (à part un qui a mal supporté les outrages du temps et a un peu moisi…). Et vu que j’avais été bien classé durant mon année de 1ère, ça m’a fallu mon instant de célébrité au lycée, avec notamment une convocation dans le bureau du proviseur :D.

Encore des maths au niveau supérieur avec une partie de la collection Le monde est mathématique, acquise il y a quelques années et qui est ressortie au moins une fois depuis. Une série de livres qui se laissent lire facilement.

En cale-livres, d’un côté on retrouve encore des maths, de la science, le seul chat que je supporte et le Magirama des Castors Juniors ! J’ai aussi le Manuel des Castors Juniors qui doit traîner quelque part.

Et de l’autre côté, le kit rafraîchissement à Japan Expo, avec une bouteille de ramune Pokémon qu’il est décemment impossible de jeter et un brumisateur nécessaire à la survie dans ce lieu surpeuplé et surchauffé.

Un petit globe terrestre pour enjoliver le tout. Je l’ai ressorti récemment pour pouvoir réfléchir sur le calcul d’hémisphères et vu que c’est joli, je l’ai laissé ici. On peut voir au tracé des frontières qu’il n’est pas tout jeune ^^.

Et puis, il y a encore ce type…