Tu sais que ça peut se calculer aussi, ce genre de conneries, chère astrophysicienne ? ;p

— Cyril [N]aud (@cyril_naud) 24 avril 2018

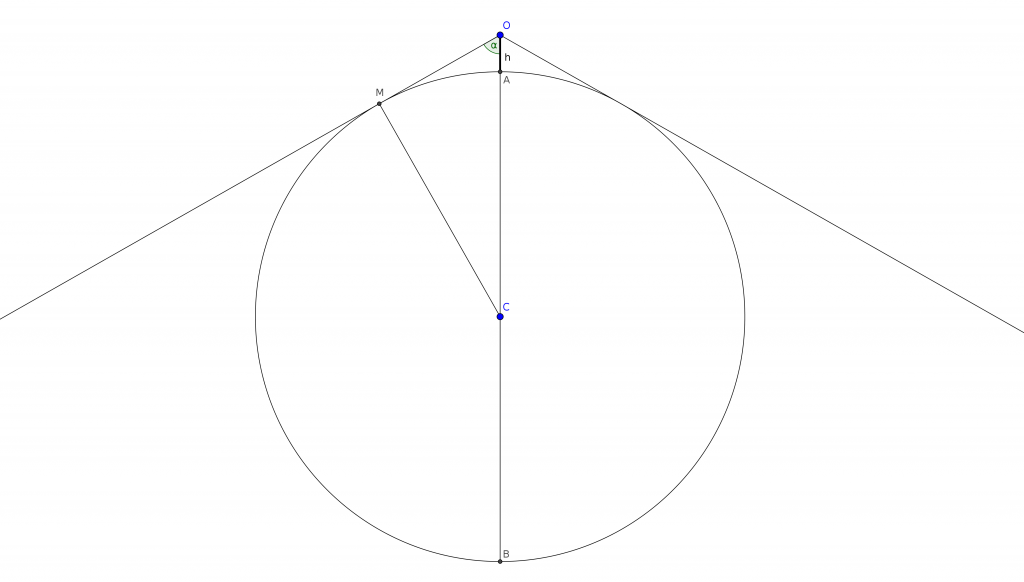
Considérons un observateur dont l’œil se trouve à une hauteur `h` du sol. La limite de ce qu’il peut voir est déterminé par les tangentes que `O` forme avec la Terre, représentée ici par un cercle de centre `C` et de rayon `R`. On prend une tangente au pif et on note `M` le point d’intersection de cette tangente avec la Terre.
Pour calculer la distance `OM`, on va utiliser la puissance d’un point par rapport à un cercle. Cela nous permet de déterminer que `OA.OB=OM²`. En sachant que `AC=BC=R`, on en déduit que `OM=sqrt(h(h+2R))`.
Vu que `OM`est une tangente au cercle, le triangle `OMC` est donc rectangle en `M`, ce qui nous permet de calculer simplement l’angle `alpha` : `tan(alpha)=(MC)/(OM)` et donc `alpha=arctan(R/sqrt(h(h+2R)))`.
On a travaillé jusque là en géométrie plane, il est désormais venu le temps de la 3D. On transforme notre angle plan `alpha` en angle solide `Omega=2pi(1-cos(alpha))=2pi(1-cos(arctan(R/sqrt(h(h+2R)))))`. En fouillant un formulaire de trigonométrie, on extrait la formule `cos(arctan(x))=1/sqrt(1+x²)`, ce qui nous permet de réduire notre valeur : `Omega=2pi(1-1/sqrt(1+(R/sqrt(h(h+2R)))²))`. On laissera au lecteur ou à la lectrice le plaisir de simplifier cette égalité afin d’obtenir `Omega=2pi(1-sqrt(h(h+2R))/(h+R))`.
Il ne reste plus qu’à calculer le volume défini par cet angle solide et pour cela, une simple règle de trois suffit. Un angle solide plein vaut `4pi` stéradians pour un volume d’Univers `V=2.54*10^(71) m^3`. Notre volume `V_i` d’Univers inobservable mesure donc `V_i=Omega/(4pi)V=(2pi(1-sqrt(h(h+2R))/(h+R)))/(4pi)V=(1-sqrt(h(h+2R))/(h+R))/2V`.

Pour l’application numérique, on utilise `R=6.371*10^6 m`. En se plaçant au niveau du sol, `h` représente la taille de l’observateur ; prenons donc `h=1.7 m`. Ce qui nous donne `V_i=0.4996V=1.269*10^(71) m^3`, soit un peu moins que ce qu’on aurait avec une Terre plate.
Prenons un peu de hauteur en nous plaçant au sommet de la Tour Eiffel. On a alors `h=324 m` et `V_i=0.495V=1.257*10^(71) m^3`. En allant sur l’Everest (`h=8848 m`), on obtient `V_i=0.474V=1.204*10^(71) m^3`. Et sur l’ISS (`h=4*10^5 m`), on a `V_i=0.331V=8.407*10^(70) m^3`.