De temps en temps arrivent sur le chan IRC du Nolife Wiki des sujets importants, comme dans ces propos d’une personne dont je tairai les multiples identités : lors d’un développement, cette boîte code un tirage aléatoire d’un entier entre 0 et 11 et, après avoir réalisé sept tirages, s’étonne d’avoir obtenu cinq fois la même valeur, s’exclame «Le hasard, c’est nul» puis sort par dépit un (1/12)⁵.

Là, mon sang de matheux ne fait qu’un tour : qu’ouïs-je ? Pourquoi cette valeur arbitraire ? Pourquoi les chapitres sur les probabilités sont-ils les derniers du programme de mathématiques de chaque année et donc non traités parce qu’il n’y a pas assez de temps ? Déterminé à en savoir plus, je décide donc de me lancer dans le calcul de cette probabilité : en tirant à sept reprises une valeur parmi douze, quelle est la probabilité d’obtenir cinq valeurs identiques ? Et tant qu’on y est, quelle est la probabilité d’obtenir X valeurs identiques ou d’obtenir sept valeurs distinctes ?

Déjà, quelques précisions et rappels.

• On considère les 12 valeurs disponibles comme équiprobables : elles ont toutes la même probabilité de sortir à chaque tirage et cette probabilité est (attention, suspense ) 1/12.
• Les tirages successifs se font avec remise : la valeur choisie lors d’un tirage est de nouveau disponible lors du tirage suivant. Si ce n’était pas le cas, la réponse à notre question serait triviale : 0 !
• L’intitulé ne dit pas que les cinq valeurs identiques doivent être une valeur donnée ! Ce biais de réflexion est bien illustré par le paradoxe des anniversaires.
• Les cinq valeurs identiques n’ont pas à être tirées à la suite : notre septuple tirage n’est pas ordonné.

Maintenant que tout ça est bien en tête, c’est parti mon kiki (ça doit bien faire deux lustres que j’ai pas utilisé cette expression :D) ! Pour répondre à notre question, nous allons créer un arbre de probabilité. Cet arbre contiendra sept niveaux, chaque niveau correspondant à un tirage. Chaque nœud ne représentera pas le tirage obtenu (l’arbre serait beaucoup BEAUCOUP BEAUCOUP trop grand et ce n’est pas ce qui nous intéresse) mais le nombre d’apparitions des valeurs tirées jusqu’alors. Petit exemple : si un nœud comporte la valeur «3-1-1», cela signifie qu’une valeur a été tirée trois fois et que deux autres valeurs ont été tirées une fois chacune; on se fiche de savoir les valeurs en question car on ne cherche pas le nombre de tirages d’une valeur donnée et parce que toutes les valeurs sont équiprobables.

Allez, c’est parti ! On prépare les sept niveaux et on commence tout à gauche.

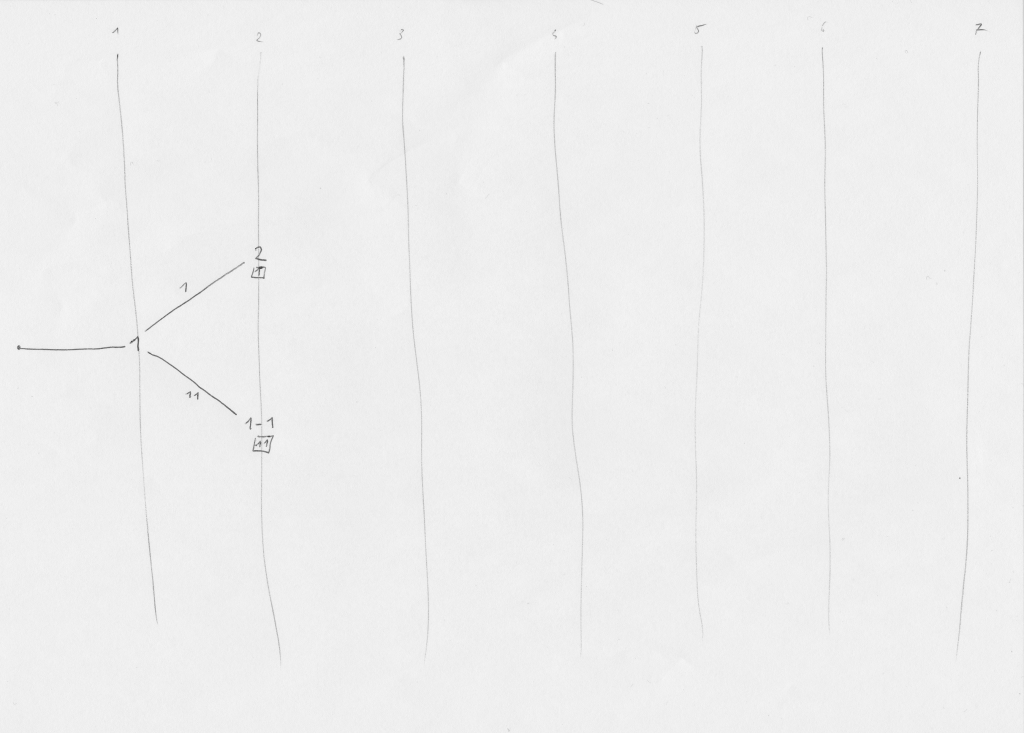
Premier tirage, on obtient une valeur et… on obtient une valeur : il n’y a qu’un seul nœud dans l’arbre à ce niveau 1, le nœud «1». Vu qu’il n’y a qu’une seule possibilité à ce stade, on considère qu’on s’en fout pour le décomptage des probabilités, ça nous épargne un facteur 12 dans les calculs.

Niveau 2 et cette fois-ci deux possibilités. Soit on tire la même valeur que précédemment (probabilité de 1/12) et on atteint le nœud «2», soit on tire une autre valeur (probabilité 11/12) pour arriver en «1-1».
Petit point notation : les nombres sur les branches indiquent la probabilité de passage par cette branche en partant du nœud de gauche et le nombre encadré sur chaque nœud indique la probabilité d’atteindre ce nœud depuis notre nœud de départ, qui est donc le nœud «1»; la probabilité d’un nœud s’obtient en faisant la somme des probabilités venant de chacune des branches qui y mène, ces probabilités étant égales au produit du nœud de départ et de la branche empruntée. Vu que toutes les probabilités sont des multiples de 1/12 et que les dits multiples sont identiques sur toutes les branches ou sur un même niveau de nœuds, on va omettre les dénominateurs sur le schéma, histoire de l’alléger. Mais il ne faudra pas oublier à la fin de diviser le résultat obtenu par 12⁶ pour obtenir la bonne probabilité, évidemment :).

Step 3. En partant de «2», soit on tire encore la même valeur déjà obtenue deux fois pour arriver en «3», soit on en tire une autre et on tombe en «2-1». Si on part de «1-1», soit on tire une des deux valeurs déjà obtenues (probabilité de 2/12) et on va en «2-1», soit on tire une des dix autres valeurs pour se rendre en «1-1-1».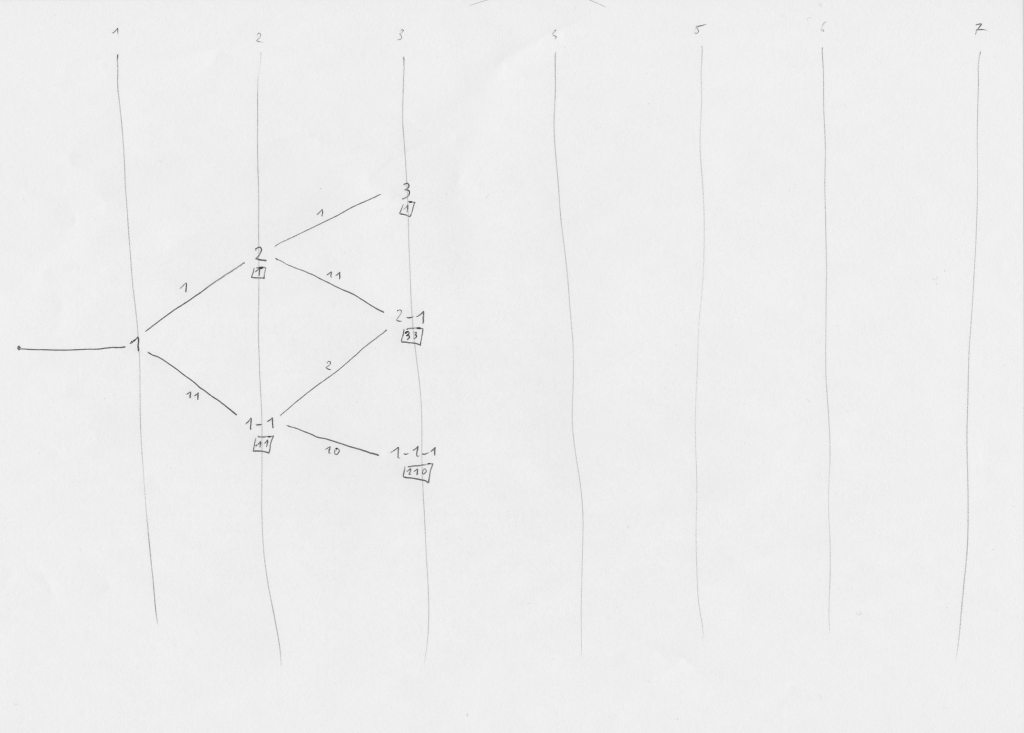

Quatrième tirage.  Rien de bien nouveau en partant des nœuds «3» et «1-1-1», qui se comportent comme leurs homologues du niveau inférieur. On va plutôt détailler les branches partant du nœud «2-1». On peut soit tirer la valeur déjà tirée deux fois (1/12), soit celle tirée une seule fois (1/12) soit une des dix autres, pas encore obtenues (10/12); ce qui nous donne trois branches partant de «2-1».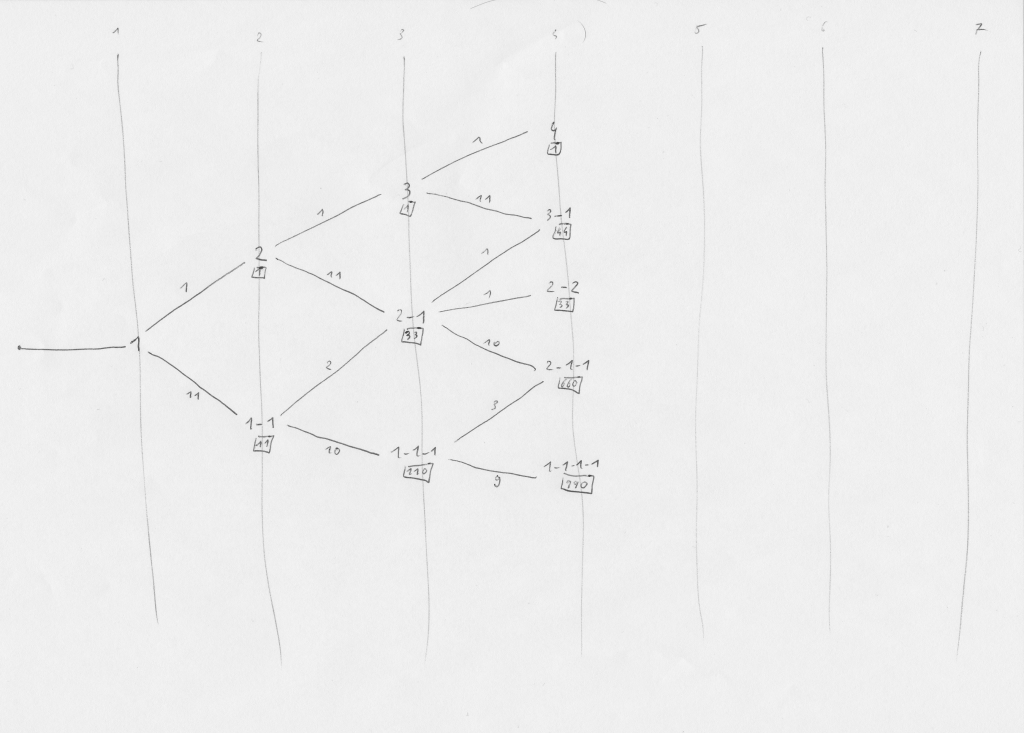

On enchaîne avec le cinquième tirage et un focus sur le nœud «2-1-1». Un des 12 tirages possibles permet de passer à «3-1-1», deux envoient sur «2-2-1» (les deux valeurs déjà tirées une seule fois) et neuf mènent à «2-1-1-1» (les valeurs pas encore tirées). Maintenant que le principe est compris, le principal challenge est de ne pas s’embrouiller avec les branches qui commencent à se croiser.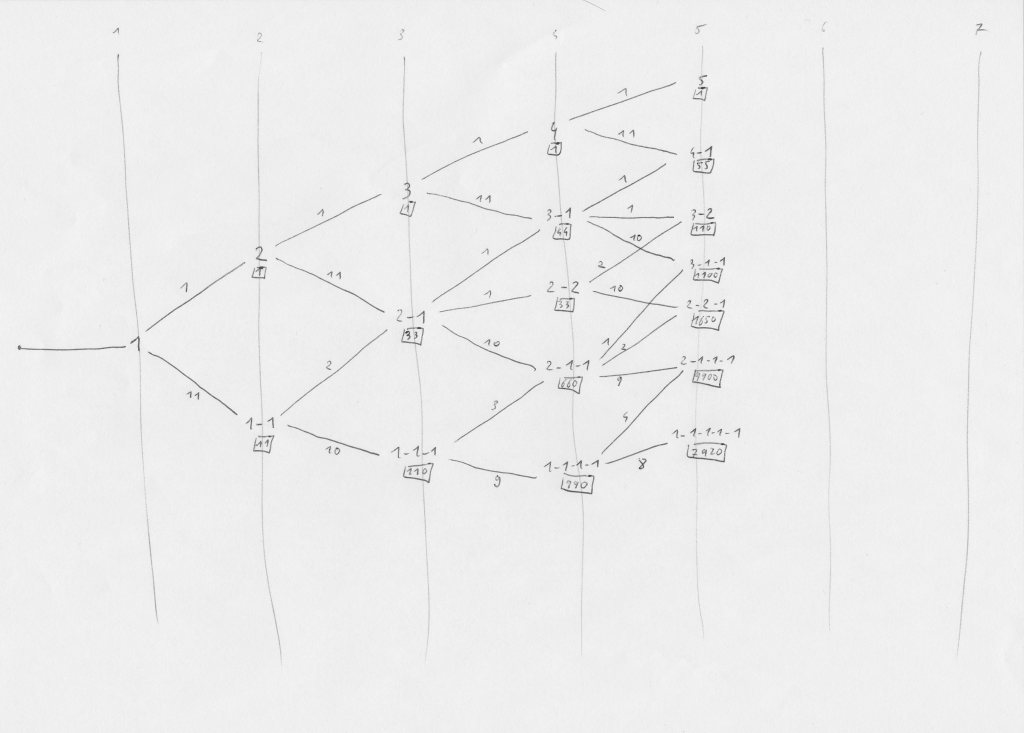

On continue sur les deux derniers niveaux. Il n’y a rien de nouveau en matière de raisonnement, j’en profite donc pour donner l’arbre final.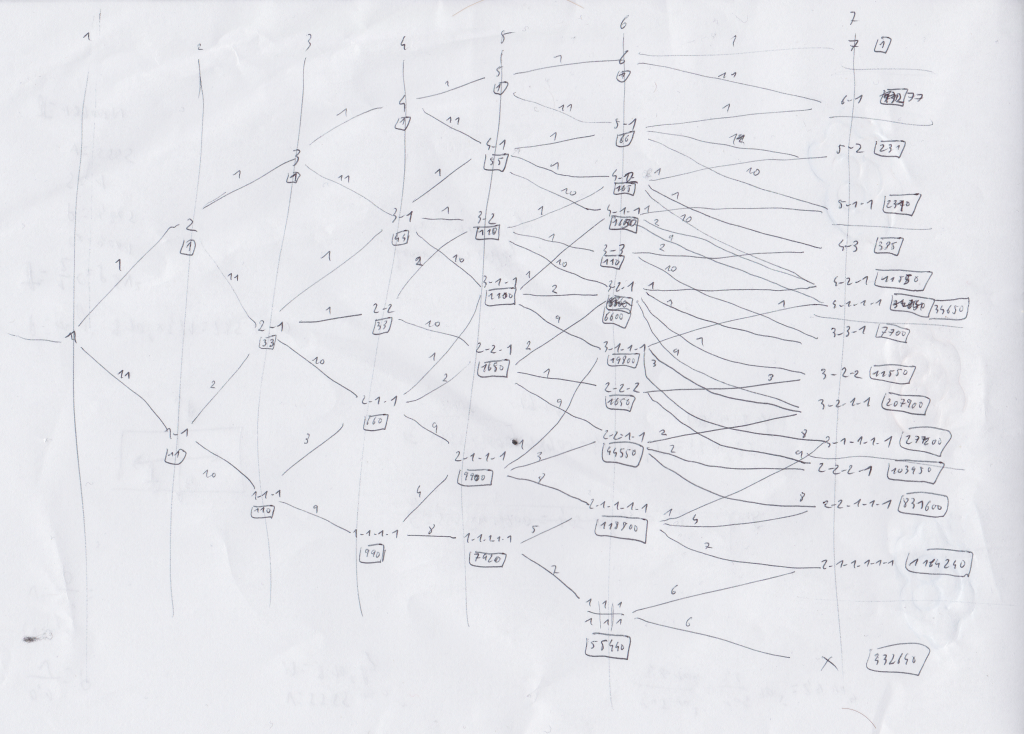On n’oublie pas de diviser par 12⁶ pour obtenir les probabilités correspondantes. Ainsi, il y a une chance sur 12⁶ d’obtenir sept valeurs identiques (et oui, 12⁶ et pas 12⁷ car il n’y a pas de contrainte de valeur au premier tirage). Pour obtenir la probabilité d’obtenir X fois la même valeur, il suffit d’ajouter les probabilités de chaque nœud où X est la plus grande valeur présente.

Ainsi, pour obtenir cinq valeurs identiques, il y a deux nœuds correspondants : «5-2» et «5-1-1». Ce qui nous donne une probabilité de (231+2310)/12⁶, soit 0,085%.

Et voici les différentes combinaisons possibles et les probabilités correspondantes.

• Sept valeurs identiques : 0,00003%
• Six valeurs identiques : 0,0026%
• Cinq valeurs identiques : 0,085%
• Quatre valeurs identiques : 1,56%
• Trois valeurs identiques : 16,89%
• Deux valeurs identiques : 70,31%
• Sept valeurs différentes : 11,14%

Une petite expérience pour terminer : il est possible de déterminer ces valeurs par l’expérimentation en réalisant un grand nombre de fois les 12 tirages et en notant le résultat obtenu à chaque fois. Vous pouvez faire ça à la main si ça vous amuse mais sinon, j’ai bricolé une page qui réalise les tirages toute seule. Il suffit d’indiquer le nombre de fois où les 12 tirages seront répétés (par défaut 10000 fois), de cliquer sur le bouton, d’attendre un peu si votre nombre est un peu gros et le nombre d’occurrences de chaque résultat est donné avec sa fréquence d’apparition, à comparer avec les probabilités données juste au dessus :).