De tous temps (non, ne partez pas, ce n’est pas une copie nulle de philo au bac), l’Homme a cherché à estimer la valeur du rapport constant entre le diamètre d’un cercle et son périmètre, qui sera plus tard appelé `pi`. Plusieurs techniques ont été établies, de l’encadrement d’un cercle par un polygone aux formules encore découvertes de nos jours, en passant par les développement en série de fonctions ou les équations de Ramanujan.

Mais il y a quelqu’un qui a eu une idée plus sympa. Georges-Louis Leclerc de Buffon a ainsi proposé une méthode permettant de calculer `pi` en lançant des aiguilles sur du parquet. Chez moi, j’ai du carrelage qui fera très bien l’affaire, l’intérêt du parquet n’étant que de définir des bandes d’une certaine largeur. Et à la place des aiguilles (c’est dangereux), je me contenterai de spaghettis (avant cuisson, dois-je vraiment le préciser ?). Mais avant de tout saloper mon intérieur, un peu de théorie.

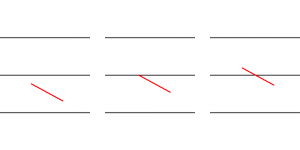
Étudions donc le lancer, le vol et l’atterrissage d’un spaghetti de longueur `s` (en fait, on se contentera juste de la situation finale, désolé) sur un parquet-carrelage dont les «lattes» sont de largeur `l`. En ayant des spaghettis plus petits qu’une latte (c’est à dire qu’on a `s<l`), il y a trois positions possibles pour notre spaghetti :

• il tient sur une latte;
• il touche la limite entre deux lattes;
• il est à cheval sur deux lattes.

Et là, paf, super schéma.

Intéressons nous à un spaghetti en particulier. Re-schéma, quelle opulence.

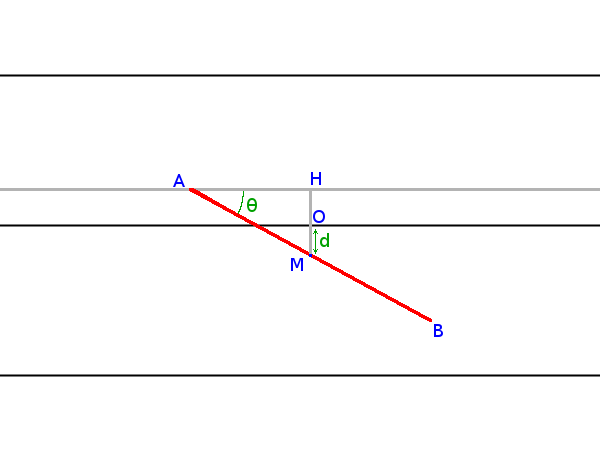
On représente notre spaghetti par un segment `AB` de centre `M` et dont l’extrémité la plus proche d’un bord de latte sera le point `A`. On trace la parallèle aux lattes passant par `A`, puis la perpendiculaire à cette droite juste créée passant par `M`. Ces deux dernières droites s’intersectent en un point `H`, formant ainsi un triangle `AHM` rectangle en `H`. On définit aussi le point `O`, intersection de la droite `(HM)` avec la frontière de latte concernée (ici, `O` est entre `H` et `M` car le spaghetti est sur deux lattes, ce n’est pas le cas s’il n’est que sur une seule latte).

On se rend alors compte qu’il y a besoin de seulement deux paramètres afin de définir s’il y a intersection ou non entre le spaghetti et la limite de latte :

• l’angle `theta` formé entre le spaghetti et la latte : en prenant le plus petit angle formé par l’intersection, cette valeur est comprise entre `0` et `pi/2`;
• la distance `d=OM` entre le milieu du spaghetti et la limite de latte, cette valeur est comprise entre `0` et `l/2`.

Allez, un peu de trigonométrie maintenant pour calculer la longueur `HM`. Un petit coup dans les sinus nous donne `sin theta = (HM)/(AM)`. Avec `AM` étant un demi-spaghetti de longueur `s/2`, on obtient donc `HM=s/2 sin theta`.

On peut maintenant se demander quelles sont les conditions pour avoir une intersection entre le spaghetti et le bord de latte. On observe rapidement qu’il faut `HM>d` et donc `d<s/2 sin theta`. On peut maintenant s’attaquer à lister les cas où il y a intersection.

Et là, on a un souci car il y a beaucoup de cas : toutes les valeurs entre `0` et `pi/2` pour `theta` croisées avec toutes les valeurs entre `0` et `l/2` pour `d`. Pour solutionner ça, faisons simple avec un espace en deux dimensions.

Toutes les solutions possibles sont représentées dans ce rectangle bleu. On a en abscisse l’angle `theta` et en ordonnée la distance `d`. On représente alors les points correspondant à notre inégalité `d<s/2 sin theta`.

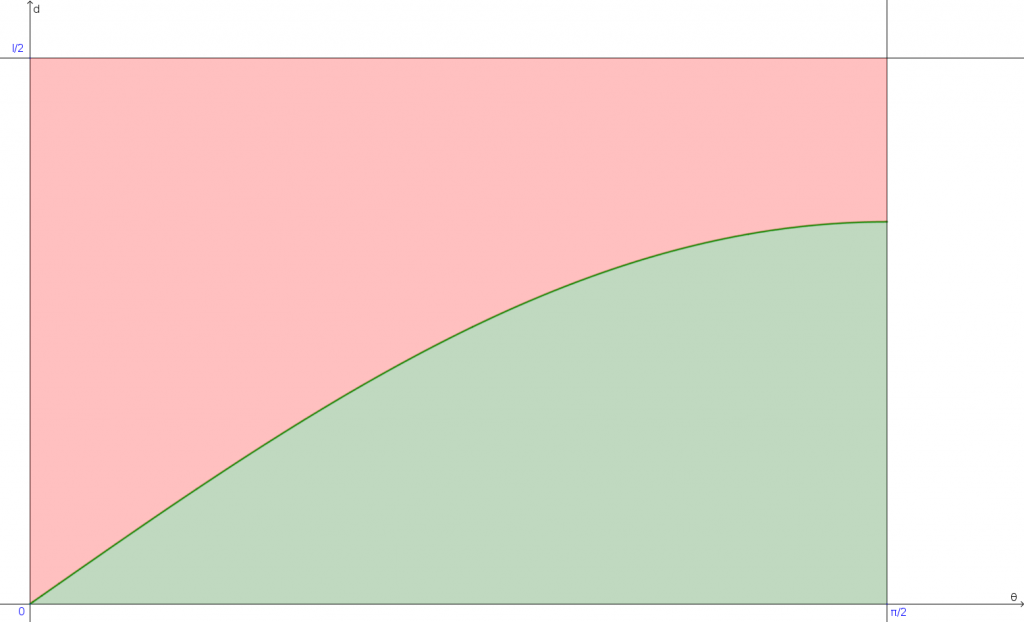La courbe verte foncée est la courbe d’équation `d=s/2 sin theta`. Tous les points résolvant l’inégalité sont représentés en vert, sous la courbe précédemment tracée. On en déduit donc que la probabilité qu’un spaghetti tombe à cheval sur deux lattes est égale à la probabilité qu’un point pris au hasard dans notre rectangle soit vert et ça, on sait calculer : il suffit d’avoir le rapport entre l’aire verte et l’aire totale.

L’aire totale, c’est très simple vu qu’il s’agit de l’aire d’un rectangle : `A=l/2xxpi/2`.  Un petit peu plus compliqué pour l’aire verte, vu qu’il faut passer par une intégrale : `A_(vert)=int_0^(pi/2) s/2 sin theta d theta`. Ça se calcule fort heureusement très vite : `A_(vert)=s/2 int_0^(pi/2) sin theta d theta` et `int_0^(pi/2) sin theta d theta=1`, d’où `A_(vert)=s/2`.

On obtient donc notre probabilité tant recherchée : `P=A_(vert)/A=(s/2)/(l/2xxpi/2)`. Ce qui nous donne `P=(2s)/(pil)` et donc `pi=(2s)/(Pl)`. Voilà, on a notre formule pour calculer `pi` !

Il n’y a plus qu’à mettre en pratique en utilisant la loi des grands nombres : si on lance un grand nombre de spaghettis, le rapport entre le nombre de spaghettis à cheval sur deux lattes et le nombre total de spaghettis sera proche de `P`, qui est la seule valeur qui nous est inconnue. Le processus pour obtenir notre estimation de `pi` est désormais clair : on lance `n` spaghettis de longueur `s` sur notre parquet dont les lattes sont de largeur `l` et on obtient `x` spaghettis à cheval sur deux lattes, on en déduit alors `pi=(2s)/(x/nl)=(2sn)/(xl)`.

Mise en pratique, donc. Voici notre parquet-carrelage, nous considérerons comme lattes les rangées de carreaux horizontales, de largeur `l=335 mm`.

On se munit d’une dose de spaghettis, de longueur `s=245 mm`.

Et voici le moment tant attendu !

Constatation des dégâts (le lancer s’est fait de la droite vers la gauche de l’image, les bandes de carreaux prises en compte apparaissent ici verticalement).

S’en suit une petite partie de mikado pour décompter les spaghettis sans tout chambouler. Notre petite expérience nous donne `x=39` spaghettis à cheval sur deux bandes, sur un total de `n=79` survivants.

Notre calcul nous donne alors `(2xx245xx79)/(39xx335)=2.963`. OK, c’est pas si loin que ça de `pi`, mais on y est pas encore. Tout simplement parce que :

• la loi des grands nombres porte bien son nom, il faut des grands nombres que notre petite centaine de spaghettis est loin d’atteindre;
• le lancer devrait être aléatoire et c’est loin d’être le cas;
• le hasard du lancer :).

L’expérience est donc à reproduire avec un plus grand nombre de spaghettis mieux lancés. À part si le comptage de spaghettis est votre grande passion dans la vie, il est possible d’utiliser des simulateurs de cette expérience de Buffon : voici par exemple celui du CNRS.